publications
publications by categories in reversed chronological order. generated by jekyll-scholar.
2026
-
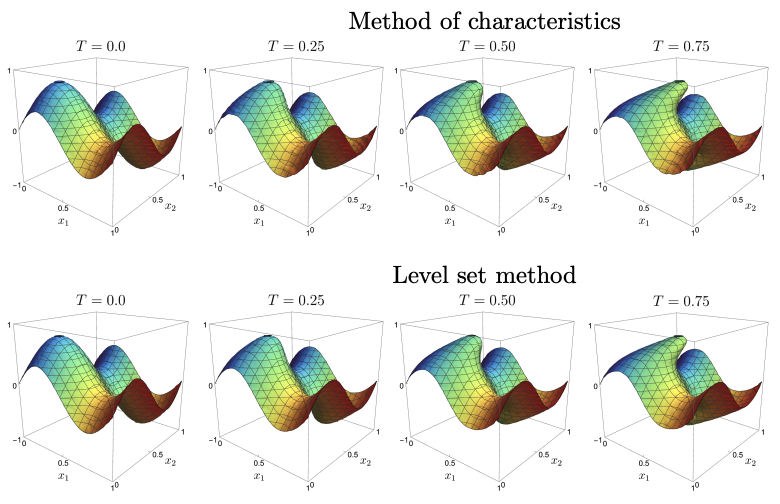 Resource-efficient quantum simulation of transport phenomena via Hamiltonian embeddingJoseph Li , Gengzhi Yang , Jiaqi Leng , and 1 more author2026
Resource-efficient quantum simulation of transport phenomena via Hamiltonian embeddingJoseph Li , Gengzhi Yang , Jiaqi Leng , and 1 more author2026Transport phenomena play a key role in a variety of application domains, and efficient simulation of these dynamics remains an outstanding challenge. While quantum computers offer potential for significant speedups, existing algorithms either lack rigorous theoretical guarantees or demand substantial quantum resources, preventing scalable and efficient validation on realistic quantum hardware. To address this gap, we develop a comprehensive framework for simulating classes of transport equations, offering both rigorous theoretical guarantees – including exponential speedups in specific cases – and a systematic, hardware-efficient implementation. Central to our approach is the Hamiltonian embedding technique, a white-box approach for end-to-end simulation of sparse Hamiltonians that avoids abstract query models and retains near-optimal asymptotic complexity. Empirical resource estimates indicate that our approach can yield an order-of-magnitude (e.g., 42×) reduction in circuit depth given favorable problem structures. We then apply our framework to solve linear and nonlinear transport PDEs, including the first experimental demonstration of a 2D advection equation on a trapped-ion quantum computer.
-
 Operator-Level Quantum Acceleration of Non-Logconcave SamplingJiaqi Leng , Zhiyan Ding , Zherui Chen , and 1 more authorPNAS, 2026
Operator-Level Quantum Acceleration of Non-Logconcave SamplingJiaqi Leng , Zhiyan Ding , Zherui Chen , and 1 more authorPNAS, 2026Sampling from probability distributions of the form σ∝e^-βV, where V is a continuous potential, is a fundamental task across physics, chemistry, biology, computer science, and statistics. However, when V is non-convex, the resulting distribution becomes non-logconcave, and classical methods such as Langevin dynamics often exhibit poor performance. We introduce the first quantum algorithm that provably accelerates a broad class of continuous-time sampling dynamics. For Langevin dynamics, our method encodes the target Gibbs measure into the amplitudes of a quantum state, identified as the kernel of a block matrix derived from a factorization of the Witten Laplacian operator. This connection enables Gibbs sampling via singular value thresholding and yields the first provable quantum advantage with respect to the Poincaré constant in the non-logconcave setting. Building on this framework, we further develop the first quantum algorithm that accelerates replica exchange Langevin diffusion, a widely used method for sampling from complex, rugged energy landscapes.
2025
-
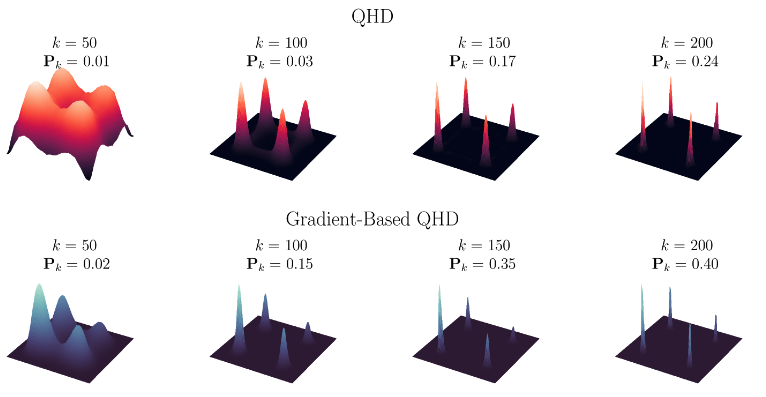 Quantum Optimization via Gradient-Based Hamiltonian DescentJiaqi Leng , and Bin ShiICML 2025, 2025
Quantum Optimization via Gradient-Based Hamiltonian DescentJiaqi Leng , and Bin ShiICML 2025, 2025With rapid advancements in machine learning, first-order algorithms have emerged as the backbone of modern optimization techniques, owing to their computational efficiency and low memory requirements. Recently, the connection between accelerated gradient methods and damped heavy-ball motion, particularly within the framework of Hamiltonian dynamics, has inspired the development of innovative quantum algorithms for continuous optimization. One such algorithm, Quantum Hamiltonian Descent (QHD), leverages quantum tunneling to escape saddle points and local minima, facilitating the discovery of global solutions in complex optimization landscapes. However, QHD faces several challenges, including slower convergence rates compared to classical gradient methods and limited robustness in highly non-convex problems due to the non-local nature of quantum states. Furthermore, the original QHD formulation primarily relies on function value information, which limits its effectiveness. Inspired by insights from high-resolution differential equations that have elucidated the acceleration mechanisms in classical methods, we propose an enhancement to QHD by incorporating gradient information, leading to what we call gradient-based QHD. Gradient-based QHD achieves faster convergence and significantly increases the likelihood of identifying global solutions. Numerical simulations on challenging problem instances demonstrate that gradient-based QHD outperforms existing quantum and classical methods by at least an order of magnitude.
-
 (Sub)Exponential Quantum Speedup for OptimizationJiaqi Leng , Kewen Wu , Xiaodi Wu , and 1 more authorPreprint, 2025
(Sub)Exponential Quantum Speedup for OptimizationJiaqi Leng , Kewen Wu , Xiaodi Wu , and 1 more authorPreprint, 2025We demonstrate provable (sub)exponential quantum speedups in both discrete and continuous optimization, achieved through simple and natural quantum optimization algorithms, namely the quantum adiabatic algorithm for discrete optimization and quantum Hamiltonian descent for continuous optimization. Our result builds on the Gilyén–Hastings–Vazirani (sub)exponential oracle separation for adiabatic quantum computing. With a sequence of perturbative reductions, we compile their construction into two standalone objective functions, whose oracles can be directly leveraged by the plain adiabatic evolution and Schrödinger operator evolution for discrete and continuous optimization, respectively.
-
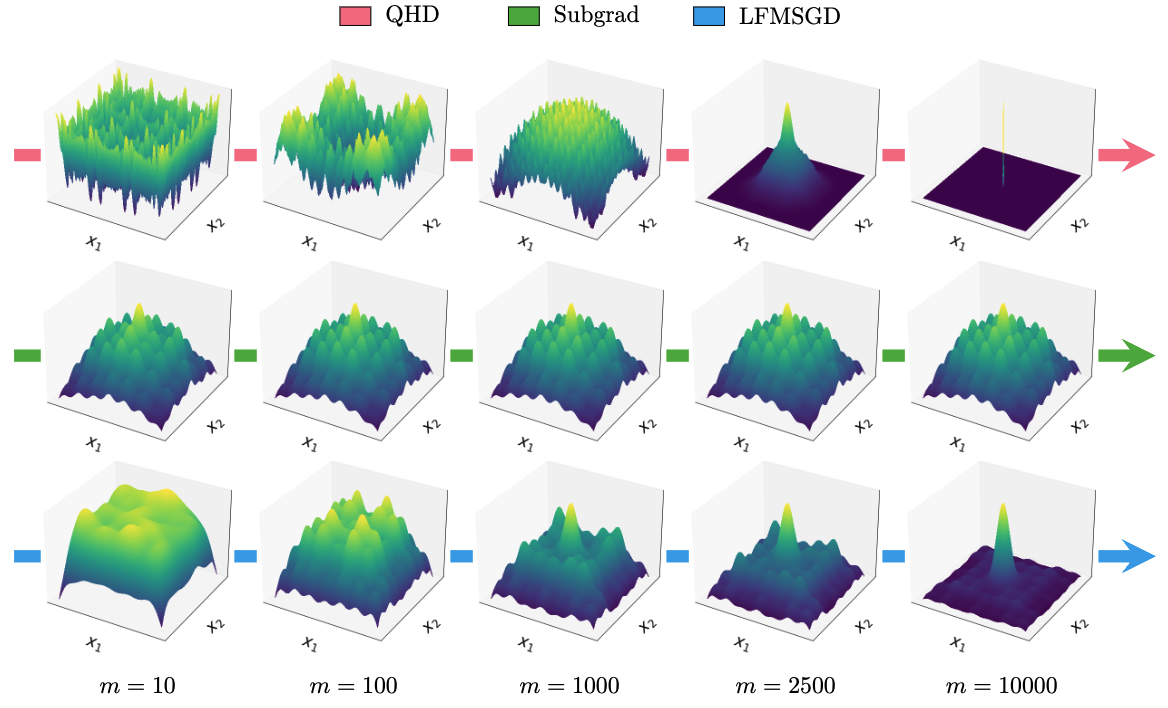 Quantum Hamiltonian Descent for Non-smooth OptimizationJiaqi Leng , Yufan Zheng , Zhiyuan Jia , and 4 more authorsPreprint, 2025
Quantum Hamiltonian Descent for Non-smooth OptimizationJiaqi Leng , Yufan Zheng , Zhiyuan Jia , and 4 more authorsPreprint, 2025Non-smooth optimization models play a fundamental role in various disciplines, including engineering, science, management, and finance. However, classical algorithms for solving such models often struggle with convergence speed, scalability, and parameter tuning, particularly in high-dimensional and non-convex settings. In this paper, we explore how quantum mechanics can be leveraged to overcome these limitations. Specifically, we investigate the theoretical properties of the Quantum Hamiltonian Descent (QHD) algorithm for non-smooth optimization in both continuous and discrete time. First, we propose continuous-time variants of the general QHD algorithm and establish their global convergence and convergence rate for non-smooth convex and strongly convex problems through a novel Lyapunov function design. Furthermore, we prove the finite-time global convergence of continuous-time QHD for non-smooth non-convex problems under mild conditions (i.e., locally Lipschitz). In addition, we propose discrete-time QHD, a fully digitized implementation of QHD via operator splitting (i.e., product formula). We find that discrete-time QHD exhibits similar convergence properties even with large time steps. Finally, numerical experiments validate our theoretical findings and demonstrate the computational advantages of QHD over classical non-smooth non-convex optimization algorithms.
-
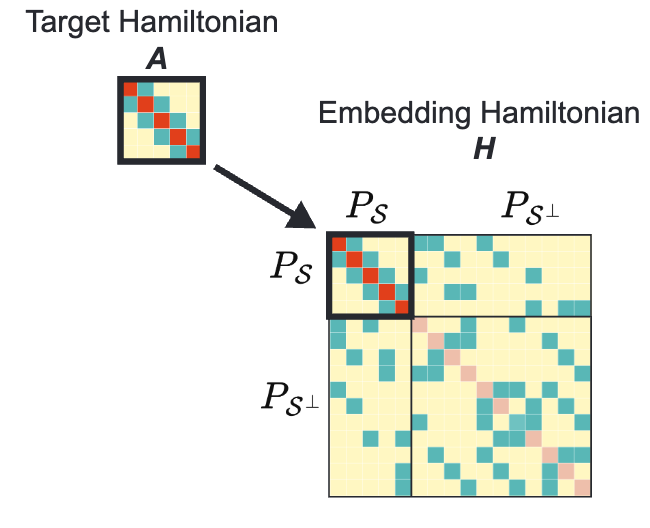 Expanding hardware-efficiently manipulable Hilbert space via Hamiltonian embeddingJiaqi Leng , Joseph Li , Yuxiang Peng , and 1 more authorQuantum, 2025
Expanding hardware-efficiently manipulable Hilbert space via Hamiltonian embeddingJiaqi Leng , Joseph Li , Yuxiang Peng , and 1 more authorQuantum, 2025Many promising quantum applications depend on the efficient quantum simulation of an exponentially large sparse Hamiltonian, a task known as sparse Hamiltonian simulation, which is fundamentally important in quantum computation. Although several theoretically appealing quantum algorithms have been proposed for this task, they typically require a black-box query model of the sparse Hamiltonian, rendering them impractical for near-term implementation on quantum devices. In this paper, we propose a technique named Hamiltonian embedding. This technique simulates a desired sparse Hamiltonian by embedding it into the evolution of a larger and more structured quantum system, allowing for more efficient simulation through hardware-efficient operations. We conduct a systematic study of this new technique and demonstrate significant savings in computational resources for implementing prominent quantum applications. As a result, we can now experimentally realize quantum walks on complicated graphs (e.g., binary trees, glued-tree graphs), quantum spatial search, and the simulation of real-space Schrödinger equations on current trapped-ion and neutral-atom platforms. Given the fundamental role of Hamiltonian evolution in the design of quantum algorithms, our technique markedly expands the horizon of implementable quantum advantages in the NISQ era.
2024
-
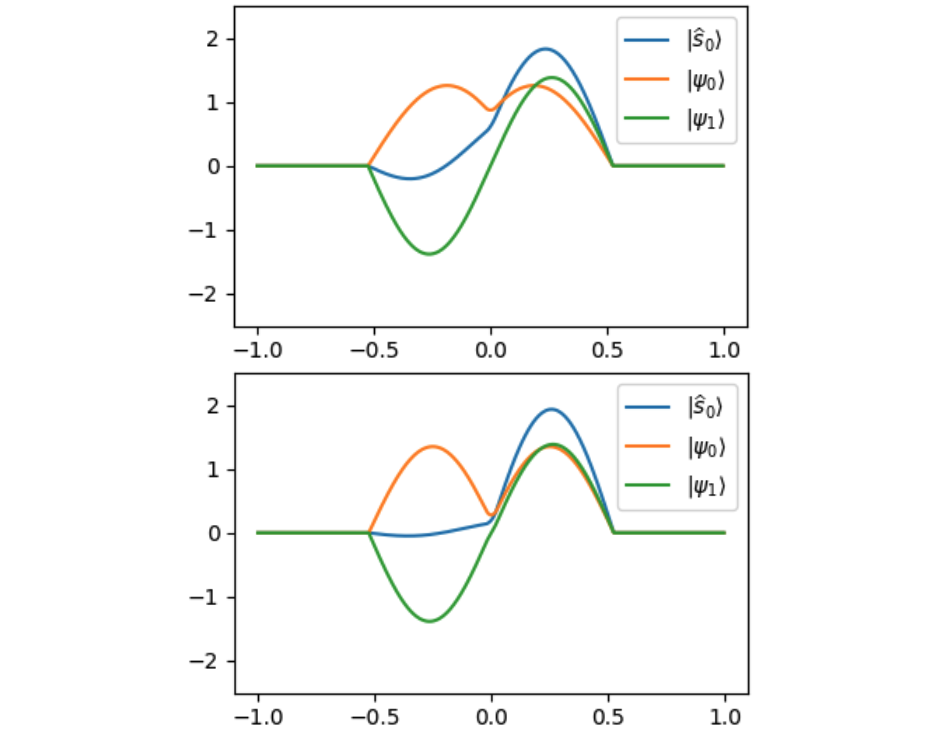 On the computational complexity of Schrödinger operatorsYufan Zheng , Jiaqi Leng , Yizhou Liu , and 1 more authorQIP 2025, 2024
On the computational complexity of Schrödinger operatorsYufan Zheng , Jiaqi Leng , Yizhou Liu , and 1 more authorQIP 2025, 2024We study computational problems related to the Schrödinger operator H = -∆+ V in the real space under the condition that (i) the potential function V is smooth and has its value and derivative bounded within some polynomial of n and (ii) V only consists of O(1)-body interactions. We prove that (i) simulating the dynamics generated by the Schrödinger operator implements universal quantum computation, i.e., it is BQP-hard, and (ii) estimating the ground energy of the Schrödinger operator is as hard as estimating that of local Hamiltonians with no sign problem (a.k.a. stoquastic Hamiltonians), i.e., it is StoqMA-complete. This result is particularly intriguing because the ground energy problem for general bosonic Hamiltonians is known to be QMA-hard and it is widely believed that StoqMA ⊊QMA.
-
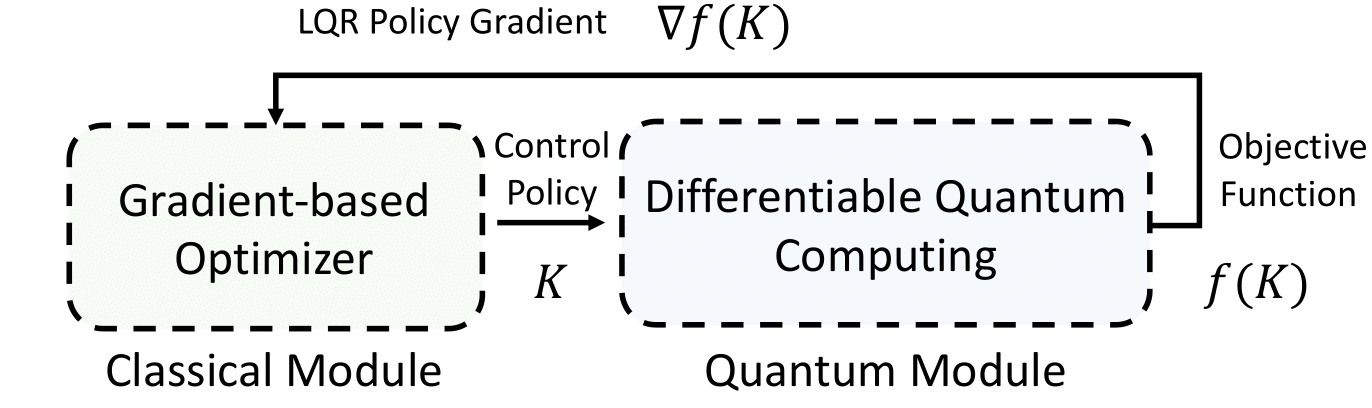 Differentiable quantum computing for large-scale linear controlConnor Clayton , Jiaqi Leng , Gengzhi Yang , and 3 more authorsNeurIPS 2025, 2024
Differentiable quantum computing for large-scale linear controlConnor Clayton , Jiaqi Leng , Gengzhi Yang , and 3 more authorsNeurIPS 2025, 2024As industrial models and designs grow increasingly complex, the demand for optimal control of large-scale dynamical systems has significantly increased. However, traditional methods for optimal control incur significant overhead as problem dimensions grow. In this paper, we introduce an end-to-end quantum algorithm for linear-quadratic control with provable speedups. Our algorithm, based on a policy gradient method, incorporates a novel quantum subroutine for solving the matrix Lyapunov equation. Specifically, we build a quantum-assisted differentiable simulator for efficient gradient estimation that is more accurate and robust than classical methods relying on stochastic approximation. Compared to the classical approaches, our method achieves a super-quadratic speedup. To the best of our knowledge, this is the first end-to-end quantum application to linear control problems with provable quantum advantage.
-
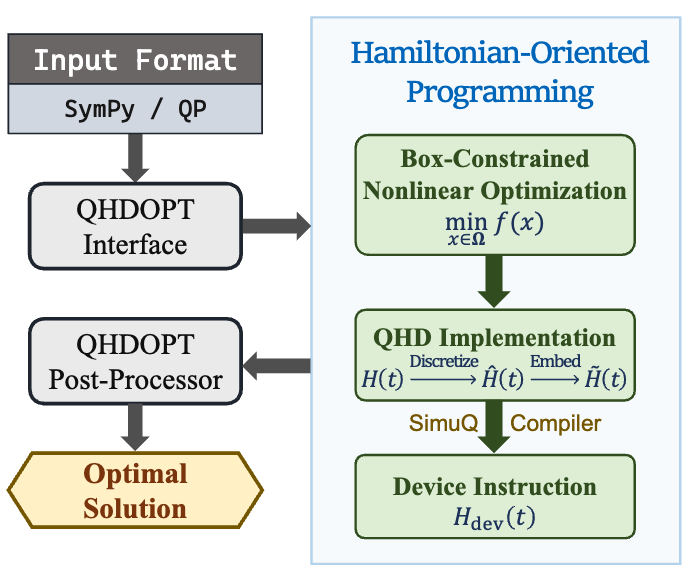 QHDOPT: A software for nonlinear optimization with quantum Hamiltonian decentSamuel Kushnir , Jiaqi Leng , Yuxiang Peng , and 2 more authorsINFORMS Journal on Computing (IJOC), 2024
QHDOPT: A software for nonlinear optimization with quantum Hamiltonian decentSamuel Kushnir , Jiaqi Leng , Yuxiang Peng , and 2 more authorsINFORMS Journal on Computing (IJOC), 2024We develop an open-source, end-to-end software (named QHDOPT), which can solve nonlinear optimization problems using the quantum Hamiltonian descent (QHD) algorithm. QHDOPT offers an accessible interface and automatically maps tasks to various supported quantum backends (i.e., quantum hardware machines). These features enable users, even those without prior knowledge or experience in quantum computing, to utilize the power of existing quantum devices for large-scale nonlinear and nonconvex optimization tasks. In its intermediate compilation layer, QHDOPT employs SimuQ, an efficient interface for Hamiltonian-oriented programming, to facilitate multiple algorithmic specifications and ensure compatible cross-hardware deployment.
2023
-
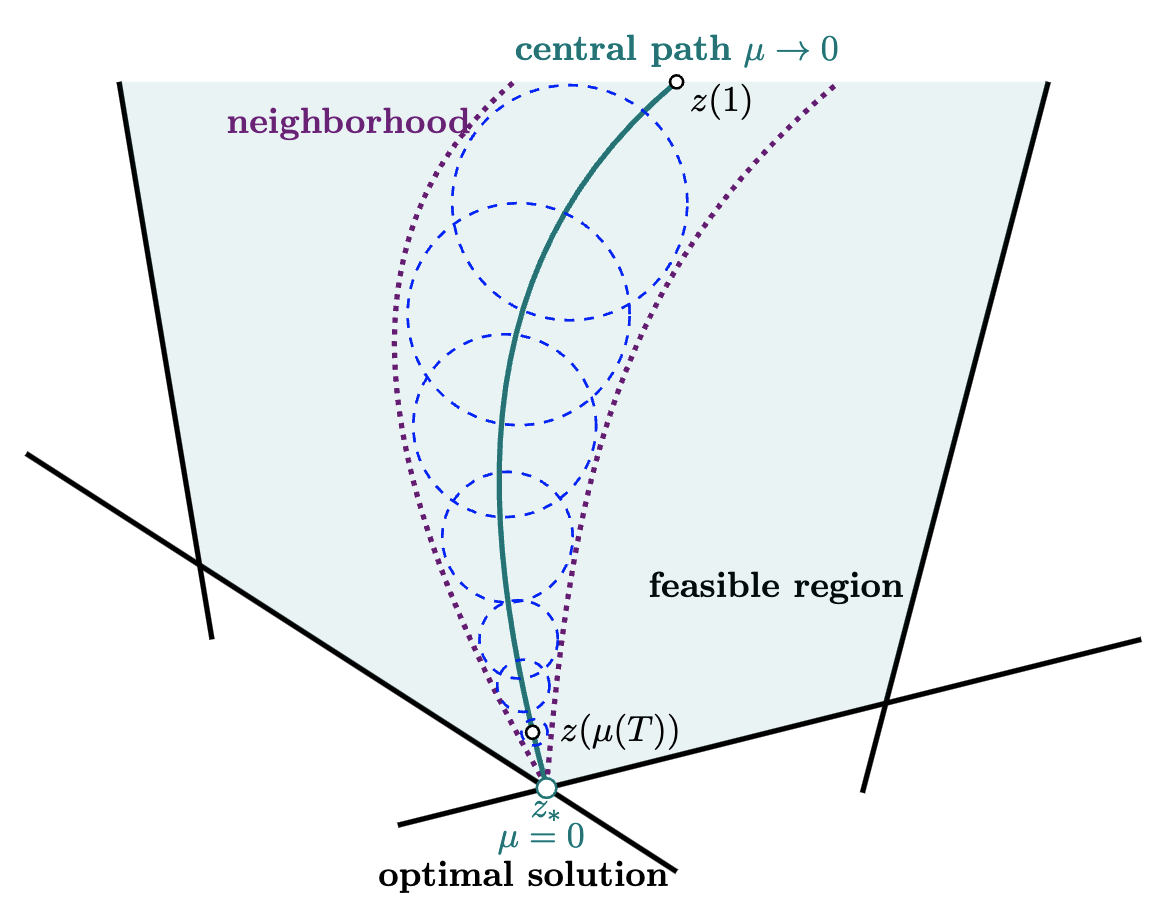 A quantum central path algorithm for linear optimizationBrandon Augustino , Jiaqi Leng , Giacomo Nannicini , and 2 more authorsQIP 2025, 2023
A quantum central path algorithm for linear optimizationBrandon Augustino , Jiaqi Leng , Giacomo Nannicini , and 2 more authorsQIP 2025, 2023We propose a novel quantum algorithm for solving linear optimization problems by quantum-mechanical simulation of the central path. While interior point methods follow the central path with an iterative algorithm that works with successive linearizations of the perturbed KKT conditions, we perform a single simulation working directly with the nonlinear complementarity equations. Combining our approach with iterative refinement techniques, we obtain an exact solution to a linear optimization problem involving m constraints and n variables using at most O ((m + n) nnz(A) κL) elementary gates and O(nnz(A) L) classical arithmetic operations, where nnz(A) is the total number of non-zero elements found in the constraint matrix, L denotes binary input length of the problem data, and κis a condition number that depends only on the problem data.
-
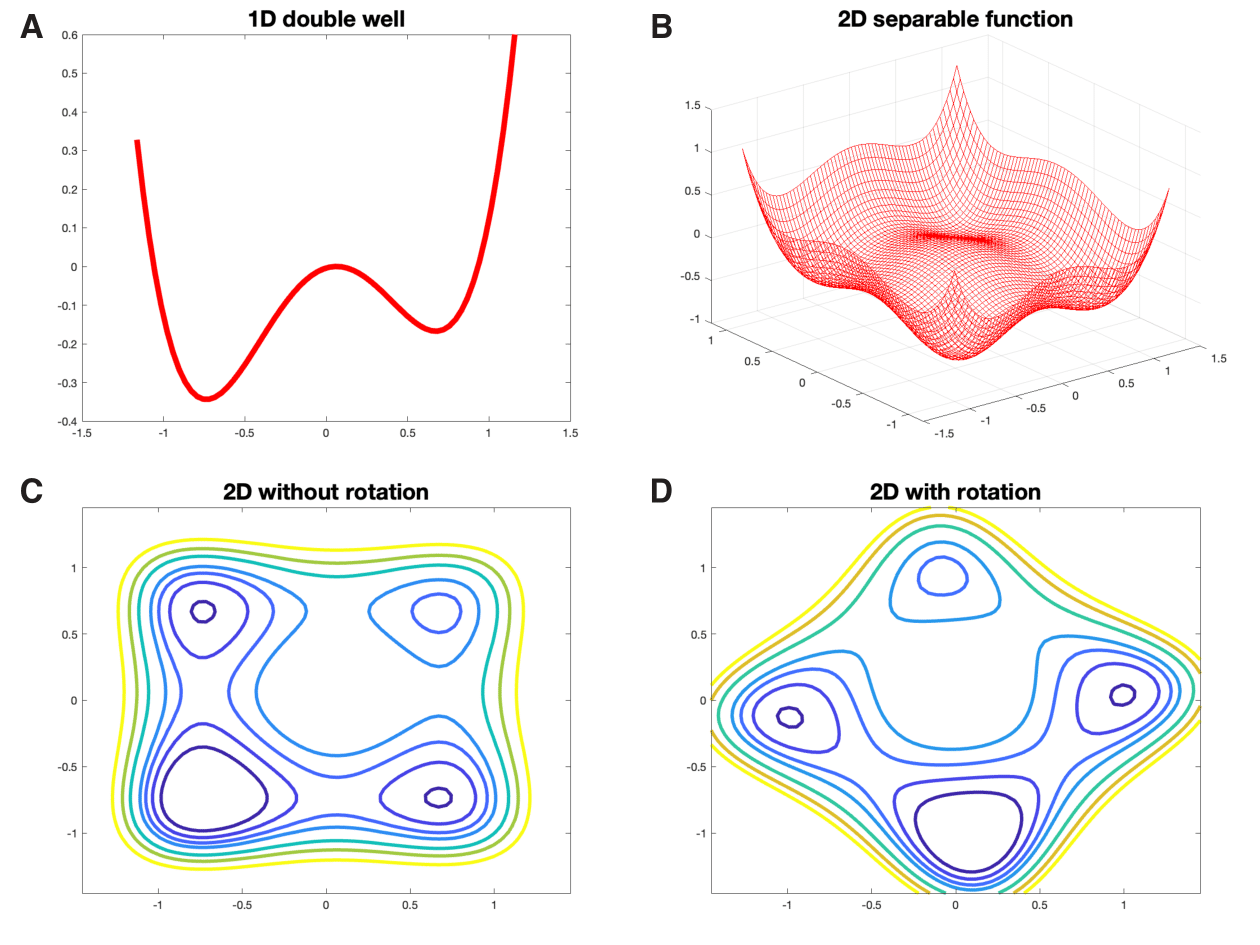 A quantum-classical performance separation in nonconvex optimizationJiaqi Leng , Yufan Zheng , and Xiaodi WuPreprint, 2023
A quantum-classical performance separation in nonconvex optimizationJiaqi Leng , Yufan Zheng , and Xiaodi WuPreprint, 2023In this paper, we identify a family of nonconvex continuous optimization instances, each d-dimensional instance with 2^d local minima, to demonstrate a quantum-classical performance separation. Specifically, we prove that the recently proposed Quantum Hamiltonian Descent (QHD) algorithm [Leng et al., arXiv:2303.01471] is able to solve any d-dimensional instance from this family using O(d^3) quantum queries to the function value and O(d^4) additional 1-qubit and 2-qubit elementary quantum gates. On the other side, a comprehensive empirical study suggests that representative state-of-the-art classical optimization algorithms/solvers (including Gurobi) would require a super-polynomial time to solve such optimization instances.
-
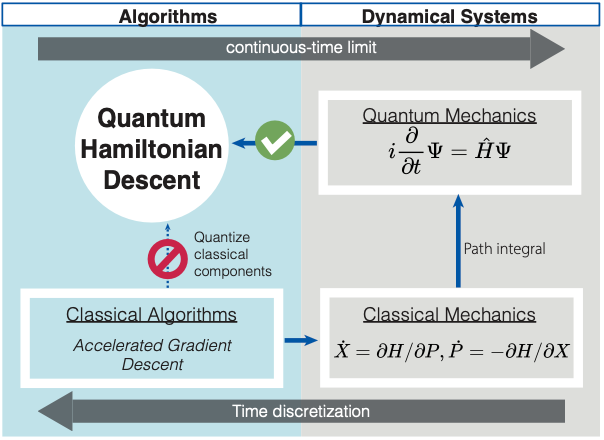 Quantum Hamiltonian DescentJiaqi Leng , Ethan Hickman , Joseph Li , and 1 more authorPreprint, 2023
Quantum Hamiltonian DescentJiaqi Leng , Ethan Hickman , Joseph Li , and 1 more authorPreprint, 2023Gradient descent is a fundamental algorithm in both theory and practice for continuous optimization. Identifying its quantum counterpart would be appealing to both theoretical and practical quantum applications. A conventional approach to quantum speedups in optimization relies on the quantum acceleration of intermediate steps of classical algorithms, while keeping the overall algorithmic trajectory and solution quality unchanged. We propose Quantum Hamiltonian Descent (QHD), which is derived from the path integral of dynamical systems referring to the continuous-time limit of classical gradient descent algorithms, as a truly quantum counterpart of classical gradient methods where the contribution from classically-prohibited trajectories can significantly boost QHD’s performance for non-convex optimization. Moreover, QHD is described as a Hamiltonian evolution efficiently simulatable on both digital and analog quantum computers. By embedding the dynamics of QHD into the evolution of the so-called Quantum Ising Machine (including D-Wave and others), we empirically observe that the D-Wave-implemented QHD outperforms a selection of state-of-the-art gradient-based classical solvers and the standard quantum adiabatic algorithm, based on the time-to-solution metric, on non-convex constrained quadratic programming instances up to 75 dimensions. Finally, we propose a "three-phase picture" to explain the behavior of QHD, especially its difference from the quantum adiabatic algorithm.
2022
-
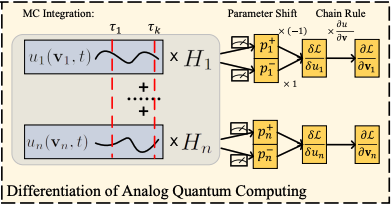 Differentiable analog quantum computing for optimization and controlJiaqi Leng , Yuxiang Peng , Yi-Ling Qiao , and 2 more authorsNeurIPS 2022, 2022
Differentiable analog quantum computing for optimization and controlJiaqi Leng , Yuxiang Peng , Yi-Ling Qiao , and 2 more authorsNeurIPS 2022, 2022We formulate the first differentiable analog quantum computing framework with specific parameterization design at the analog signal (pulse) level to better exploit near-term quantum devices via variational methods. We further propose a scalable approach to estimate the gradients of quantum dynamics using a forward pass with Monte Carlo sampling, which leads to a quantum stochastic gradient descent algorithm for scalable gradient-based training in our framework. Applying our framework to quantum optimization and control, we observe a significant advantage of differentiable analog quantum computing against SOTAs based on parameterized digital quantum circuits by orders of magnitude.
- QuantumQuantum simulation of real-space dynamicsAndrew M Childs , Jiaqi Leng , Tongyang Li , and 2 more authorsQuantum, 2022
Quantum simulation is a prominent application of quantum computers. While there is extensive previous work on simulating finite-dimensional systems, less is known about quantum algorithms for real-space dynamics. We conduct a systematic study of such algorithms. In particular, we propose quantum algorithms to simulate the dynamics of a d-dimensional Schrödinger equation with ηparticles. Compared to the best previous results, our quantum algorithms achieve exponential improvements in several problem parameters. We give applications to several computational problems, including faster real-space simulation of quantum chemistry, rigorous analysis of discretization error for simulation of a uniform electron gas, and a quadratic improvement to a quantum algorithm for escaping saddle points in nonconvex optimization.
2021
-
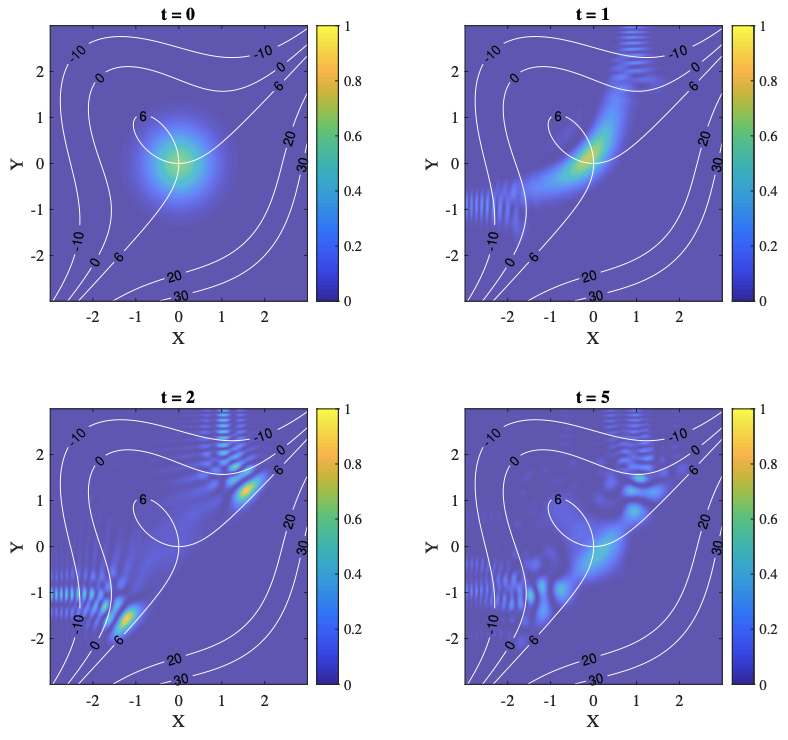 Quantum algorithms for escaping from saddle pointsChenyi Zhang , Jiaqi Leng , and Tongyang LiQuantum, 2021
Quantum algorithms for escaping from saddle pointsChenyi Zhang , Jiaqi Leng , and Tongyang LiQuantum, 2021We initiate the study of quantum algorithms for escaping from saddle points with provable guarantee. Compared to classical algorithms by Jin et al., our quantum algorithm is polynomially better in terms of log(n) (n is the problem dimension) and matches its complexity in terms of 1/ε. Technically, our main contribution is the idea of replacing the classical perturbations in gradient descent methods by simulating quantum wave equations, which constitutes the improvement in the quantum query complexity with log(n) factors for escaping from saddle points. We also show how to use a quantum gradient computation algorithm due to Jordan to replace the classical gradient queries by quantum evaluation queries with the same complexity. Finally, we also perform numerical experiments that support our theoretical findings.