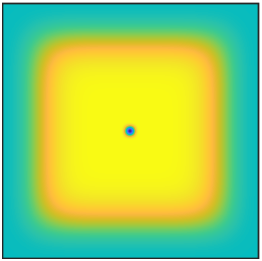
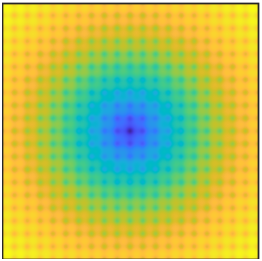
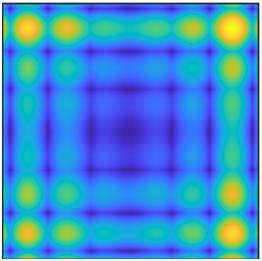
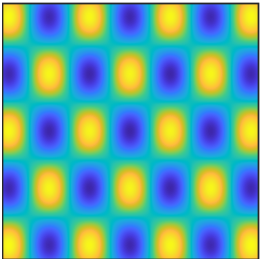
We demonstrate the difference between QHD and other algorithms with interactive 3D visualizations and the three-phase diagrams (for details, see Executive Summary).

Test functions & Methodology

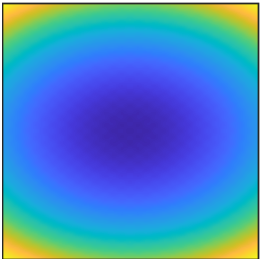
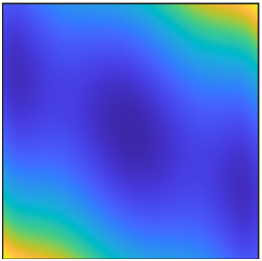
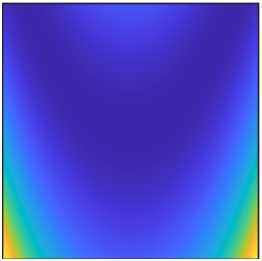
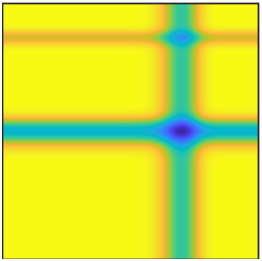
We gathered a set of 22 continuous two-dimensional test functions from the optimization literature (e.g., ref1, ref2, ref3). Functions are divided into five categories based on their diversified landscapes: (1) Ridges and Valleys: a mix of functions with steep barriers and/or valleys; (2) Basin: Most of the domain is at a low objective value, so exhaustive search for would yield a small improvement in objective value. The gradient signal may be weak in most of the basin; (3) Flat: most of the domain is at a high objective value, so exhaustive search would yield a large improvement in objective value. The gradient signal may be weak, useless, or misleading over most of the domain; (4) Studded: highly non-convex functions, such that the gradient may be large in magnitude but misleading due to high local curvature. Marked by many local minima imposed on a base shape; (5) Simple: Functions solved efficiently by a classical gradient method.

For comparable performance, we normalize all objective functions. Details are available here. We compare QHD with the Quantum Adiabatic Algorithm (QAA), stochastic gradient descent (SGD) and Nesterov’s accelerated gradient descent (NAGD) on objective functions with a variety of landscape features. QHD and QAA are numerically simulated (resolution: QHD = 1/256, QAA = 1/128).

For presentation, the surface plots are compressed to a \(64 \times 64\) grid by taking the sum of probability over square tiles.